Appearance
10.1 基础数据结构
10.1.1 数组(Array)
数组是可以在内存中连续存储多个元素的结构,在内存中的分配也是连续的 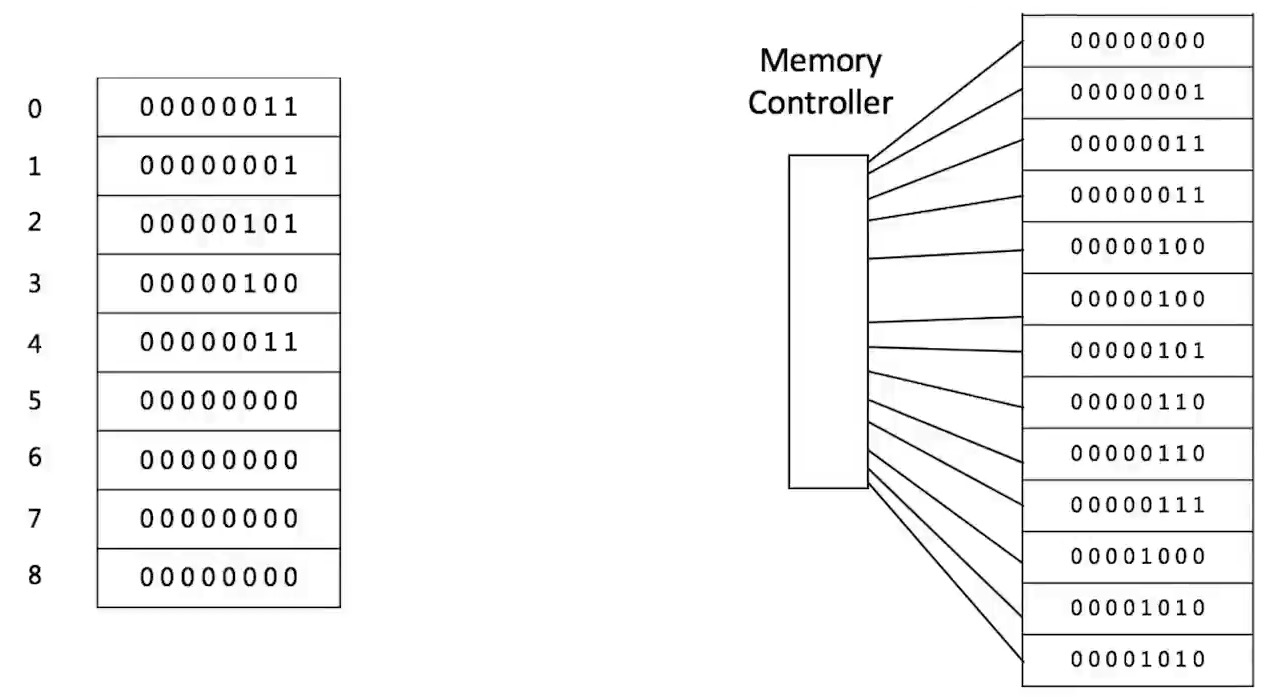
优点:
- 按照索引查询元素速度快
- 按照索引遍历数组方便
缺点:
- 数组的大小固定后就无法扩容了
- 数组只能存储一种类型的数据
- 添加,删除的操作慢,因为要移动其他的元素
适用场景:
频繁查询,很少插入或删除的情况,且对存储空间要求不大
10.1.2 链表(Linked List)
链表是物理存储单元上非连续的、非顺序的存储结构,数据元素的逻辑顺序是通过链表的指针地址实现,每个元素包含两个结点,一个是存储元素的数据域 (内存空间),另一个是指向下一个结点地址的指针域。根据指针的指向,链表能形成不同的结构,例如单链表,双向链表,循环链表等 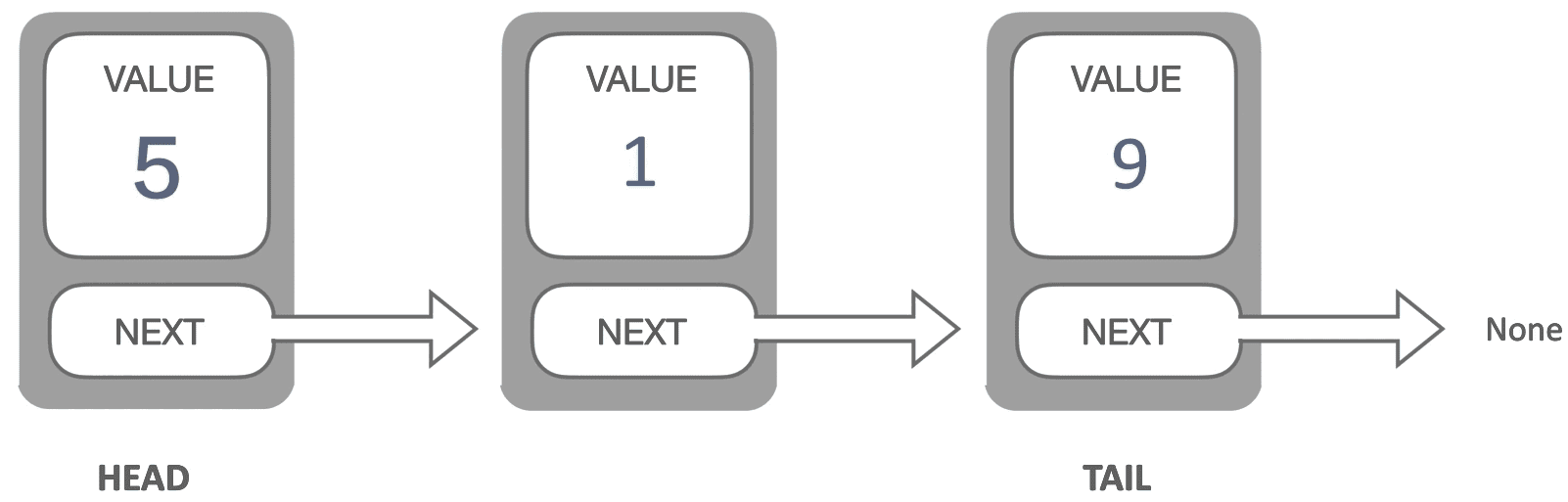
优点:
- 链表是很常用的一种数据结构,不需要初始化容量,可以任意加减元素
- 添加或者删除元素时只需要改变前后两个元素结点的指针域指向地址即可,所以添加,删除很快
缺点:
- 因为含有大量的指针域,占用空间较大
- 查找元素需要遍历链表来查找,非常耗时(使用
跳表优化查询速度)
适用场景:
频繁插入或删除,很少查询的情况,且对存储空间要求不大
10.1.3 栈(Stack)
栈,也叫堆栈,是一种特殊的线性表,仅能在线性表的一端操作,栈顶允许操作,栈底不允许操作。 栈的特点是:先进后出,或者说是后进先出,从栈顶放入元素的操作叫入栈,取出元素叫出栈 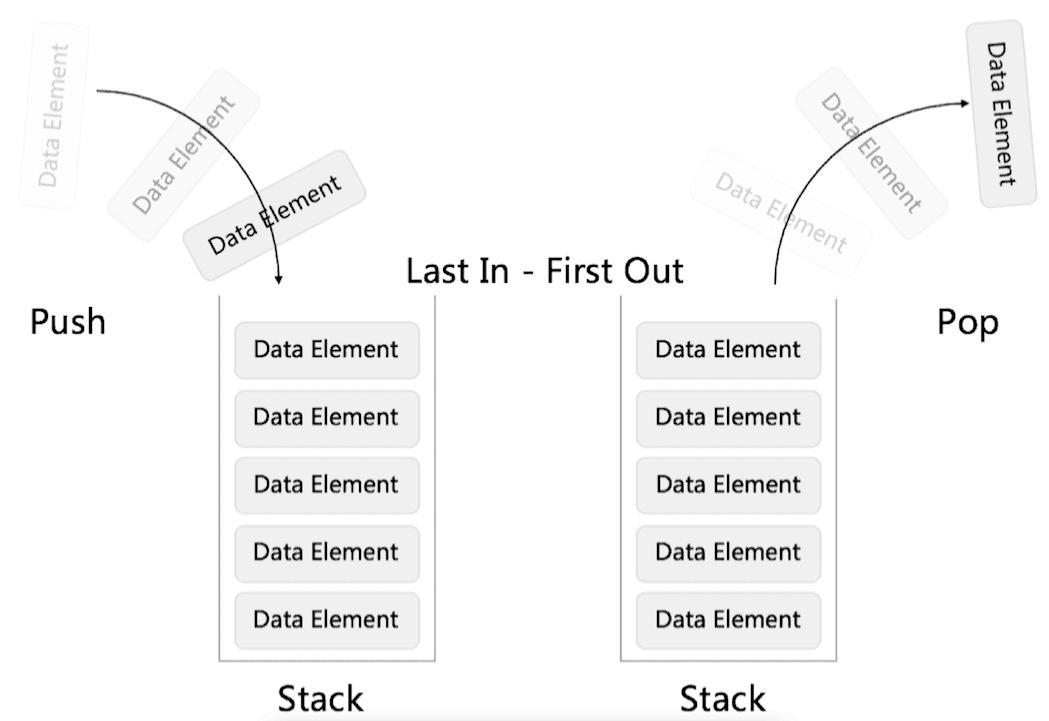
优点:
- 提供后进先出的存取方式
缺点:
- 存取其他项都很慢
适用场景
递归功能方面的场景,例如斐波那契数列
10.1.4 队列(Queue)
队列与栈一样,也是一种线性表,不同的是,队列可以在一端添加元素,在另一端取出元素,也就是:先进先出。从一端放入元素的操作称为入队,取出元素为出队。 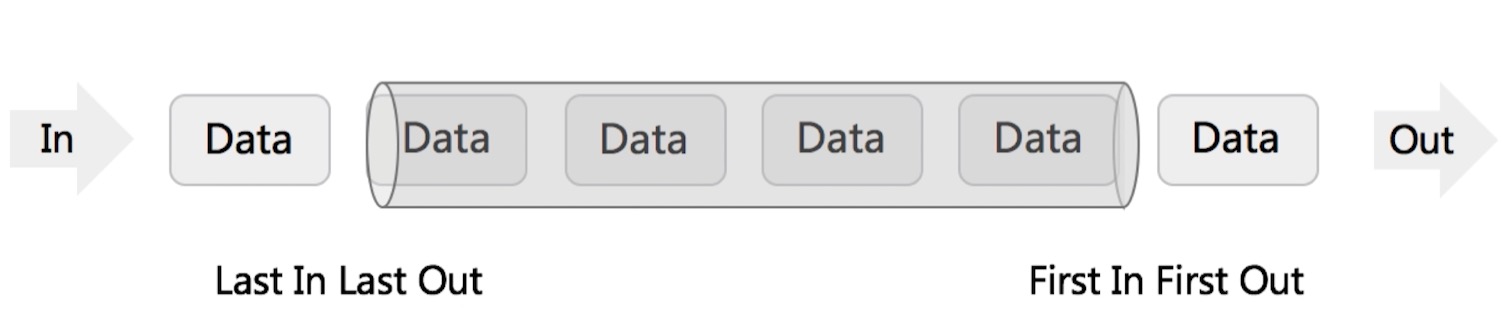
优点:
- 提供先进先出的存取方式
缺点:
- 存取其他项都很慢
适用场景
多线程阻塞队列管理
10.1.5 树(Tree)
树是一种数据结构,它是由n(n>=1)个有限节点组成一个具有层次关系的集合。把它叫做 “树” 是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
- 它具有以下的特点:
- 每个节点有零个或多个子节点
- 没有父节点的节点称为根节点
- 每一个非根节点有且只有一个父节点
- 除了根节点外,每个子节点可以分为多个不相交的子树
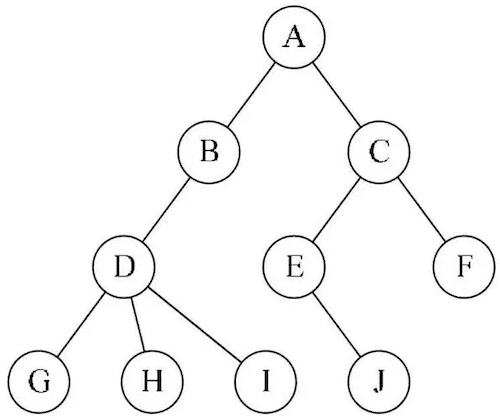
- 二叉树特点:
- 每个结点最多有两颗子树,结点的度最大为2
- 左子树和右子树是有顺序的,次序不能颠倒
- 即使某结点只有一个子树,也要区分左右子树
- 二叉搜索树特点:
- 左子树上的所有节点值均小于它的根节点的值
- 右子树上的所有节点值均大于它的根节点的值
- 左右子树也分别符合以上两点
优点:
- 查找,插入,删除都快
- 既有链表的好处,也有数组的好处
缺点:
适用场景:
二叉树既有链表的好处,也有数组的好处,是两者的优化方案,在处理大批量的动态数据方面非常有用。
10.1.6 哈希表(Hash table)
哈希表,也叫散列表,是根据关键码和值 (key和value) 直接进行访问的数据结构,通过key和value来映射到集合中的一个位置,这样就可以很快找到集合中的对应元素(哈希冲突:如果key值重复则通常用链表存储相同key值对应的value)。 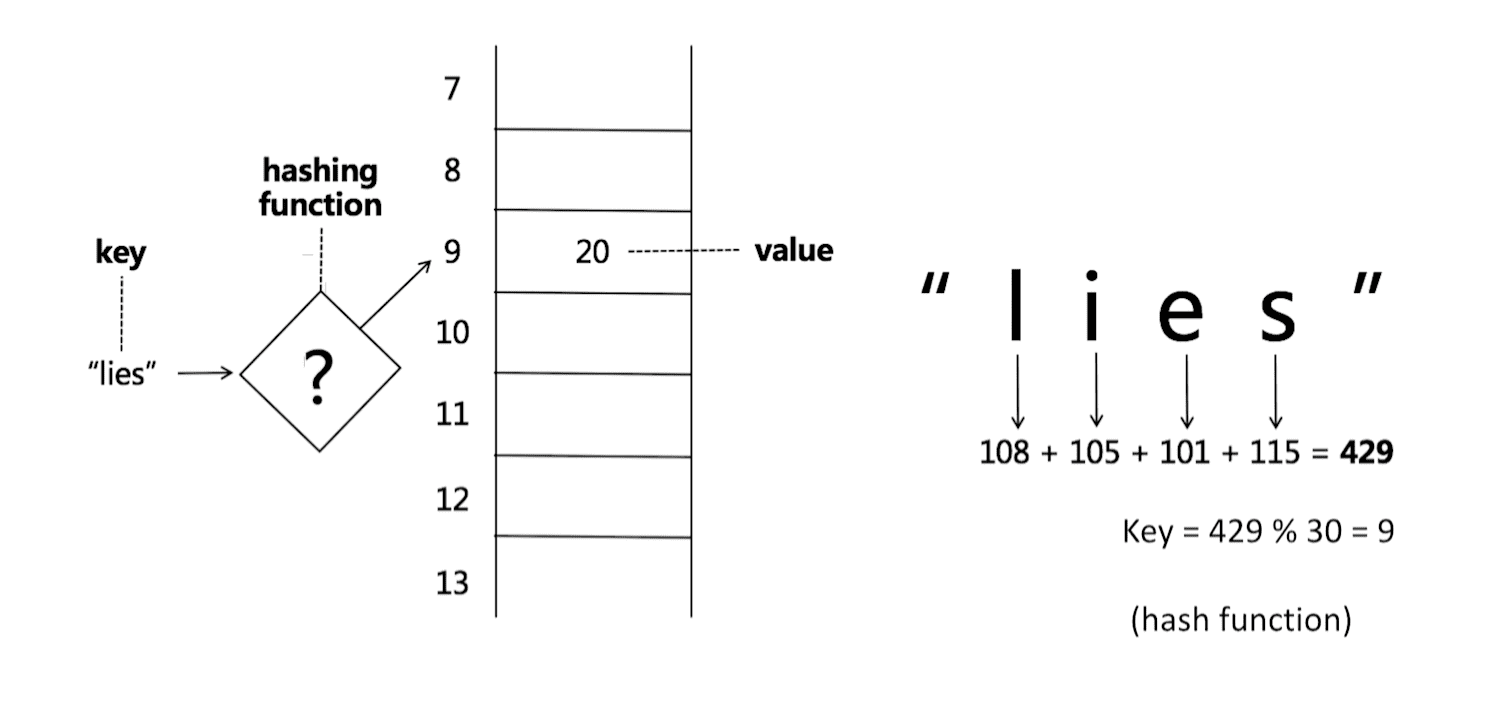
优点:
- 如果关键字已知则存取速度极快
缺点:
- 删除慢,如果不知道关键则存取很慢,对存储空间使用不充分
适用场景:
Map、Set
10.1.7 堆(Heap)
堆是一种比较特殊的数据结构,可以被看做一棵树的数组对象。
- 具有以下的性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值;
- 堆总是一棵完全二叉树。
- 将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等。
将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等。
堆的定义如下:n个元素的序列{k1,k2,ki,…,kn}当且仅当满足下关系时,称之为堆。 (ki <= k2i,ki <= k2i+1)或者(ki >= k2i,ki >= k2i+1), (i = 1,2,3,4…n/2),满足前者的表达式的成为小顶堆,满足后者表达式的为大顶堆,这两者的结构图可以用完全二叉树排列出来,示例图如下:
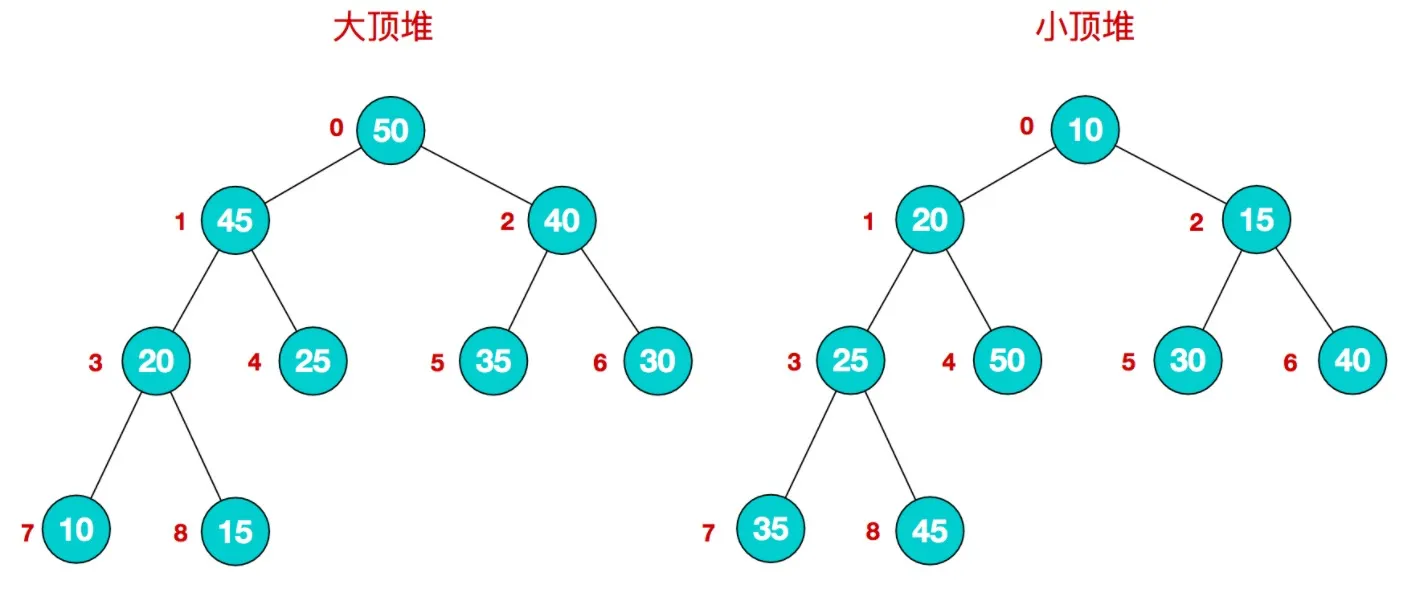
优点:
- 插入,删除块,对最大数据的项存取很快
缺点:
- 对其他数据项存取很慢
适用场景:
因为堆有序的特点,一般用来做数组中的排序,称为堆排序。
10.1.8 图(Graph)
图是由结点的有穷集合V和边的集合E组成。其中,为了与树形结构加以区别,在图结构中常常将结点称为顶点,边是顶点的有序偶对,若两个顶点之间存在一条边,就表示这两个顶点具有相邻关系。
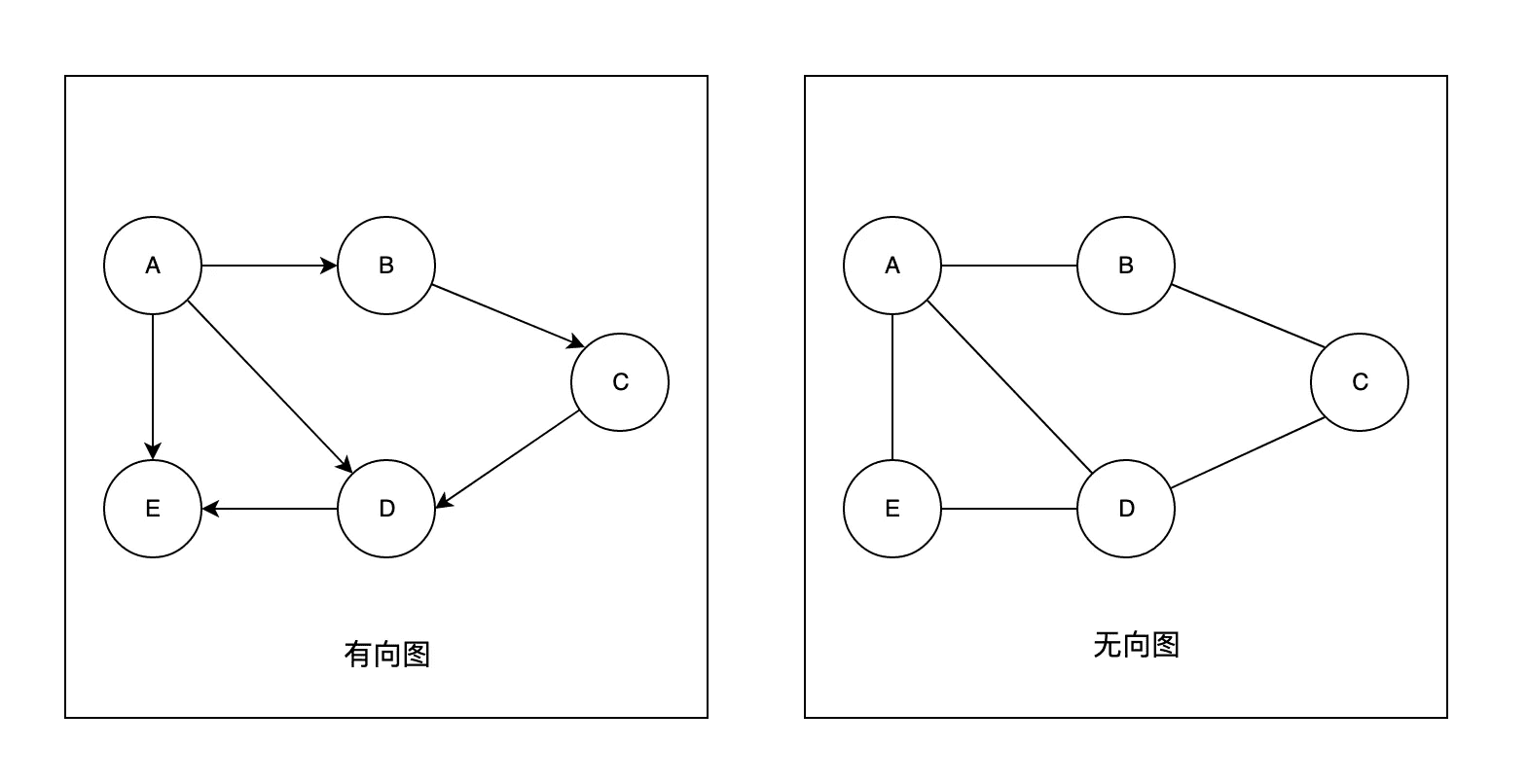
图是一种比较复杂的数据结构,在存储数据上有着比较复杂和高效的算法,分别有邻接矩阵 、邻接表、十字链表、邻接多重表、边集数组等存储结构,这里不做展开,读者有兴趣可以自己学习深入。
优点:
缺点:
适用场景:
10.2 时间复杂度与空间复杂度
时间:是指执行当前算法所消耗的时间 空间:是指执行当前算法需要占用多少内存空间 负责度:是指算法随着执行次数的增长,所花费的时间、空间的增长趋势
10.2.1 时间复杂度
公式:T(n) = O(f(n))
f(n):表示每行代码执行次数之和 去掉常数项和系数、只保留复杂度最大项
常见的时间复杂度量级有:
- 常数阶
O(1)无论代码执行了多少行,只要是没有循环等复杂结构,那这个代码的时间复杂度就都是O(1)
js
int i = 1;
int j = 2;
++i;
j++;
int m = i + j;- 对数阶
O(logN)
js
int i = 1;
while(i<n)
{
i = i * 2;
}- 线性阶
O(n)
js
for(i=1; i<=n; ++i)
{
j = i;
j++;
}- 线性对数阶
O(nlogN)
js
for(m=1; m<n; m++)
{
i = 1;
while(i<n)
{
i = i * 2;
}
}- 平方阶
O(n²)
js
for(x=1; i<=n; x++)
{
for(i=1; i<=n; i++)
{
j = i;
j++;
}
}- 立方阶
O(n³) - K次方阶
O(n^k) - 指数阶
(2^n)
时间负责度优化方向
升维、空间换时间
10.2.2 空间复杂度
公式:T(n) = O(f(n))
f(n):表示每行代码占用的空间大小之和 去掉常数项和系数、只保留复杂度最大项
常见的时间复杂度量级有:
- 常数阶
O(1)只要不会因为算法里的执行,导致额外的空间增长,就算是一万行,空间复杂度也是O(1)
js
function foo(){
let n = 1
let b = n * 100
if(b === 100){
console.log("开始吃糖")
}
console.log("我吃了1颗糖")
console.log("我吃了2颗糖")
......
console.log("我吃了10000颗糖")
}- 线性阶
O(n)
js
function foo(n){
let arr = []
for( let i = 1; i < n; i++ ) {
arr[i] = i
}
}- 平方阶
O(n²)O(n²) 这种空间复杂度一般出现在比如二维数组,或是矩阵的情况
js
let arr = [
[1,2,3,4,5],
[1,2,3,4,5],
[1,2,3,4,5]
]- 阶乘
O(n!)